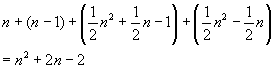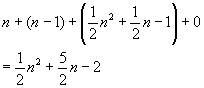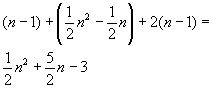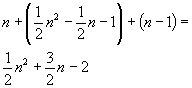Konrad-Adenauer-Gymnasium Langenfeld
Informatik Grundkurs Q1
Bewertung des direkten Auswählens
Hinweis: Dieses Dokument ist nicht zum Selbststudium geeignet. Hier sind
Erklärungen des Unterrichts notwendig, die aber nur sehr schwer aufzuschreiben
sind. Daher dient diese Seite lediglich der Dokumentation.
Analyse der Zeitkomplexität
Prinzipiell sind zwei ineinander geschachtelte Schleifen zu durchlaufen. Die
äußere Schleife (durch step repräsentiert) wird (n-1)-mal durchlaufen. Die
innere Schleife (in sort repräsentiert durch j) wird (n-i)-mal durchlaufen. Sie
ist damit abhängig vom Wert von i.
(I) Wertzuweisungen vom int-Typ:
- Zuweisungen an die Steuervariable der äußeren Schleife(aktuell): n-mal
(einmal zusätzlich, da ja auch beim letzten falschen Vergleich noch einmal
zugewiesen wird)
- Zuweisungen an platz: (n-1)-mal
- Zuweisungen an die Steuervariable j der inneren Schleife:
(jeweils +1, da für den falschen Vergleich einmal mehr zugewiesen wird)
|
aktuell = 0 |
n |
Wertzuweisungen |
|
aktuell = 1 |
n-1 |
Wertzuweisungen |
|
aktuell = 2 |
n-2 |
Wertzuweisungen |
|
¼ |
¼ |
¼ |
|
aktuell = n-2 |
2 |
Wertzuweisungen |
Diese Anzahlen müssen addiert werden. Mit der Summenformel ergibt sich
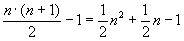
als Gesamtzahl dieser Wertzuweisungen.
- Die Anzahl der weiteren Wertzuweisungen hängt von Bedingungen ab. Daher
können wir keine einheitliche Zahl für alle Fälle angeben. Insofern
beschränken wir uns auf den günstigsten (best case) und ungünstigsten (worst
case) Fall. Allerdings darf nicht einfach das arithmetische Mittel genommen
werden, sondern die Analyse müsste für alle n! Fälle durchgespielt werden.
Das ist aber für uns zu aufwendig.
[Für Interessierte: Niklaus Wirth: Algorithmen und Datenstrukturen. Teubner
Stuttgart 1975. S84f.]
Worst Case:
Die If-Bedingung feld[j]<kleinstes ist stets erfüllt. Die abhängigen
Anweisungen werden ausgeführt.
Anzahl: 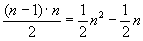
Best Case:
Die If-Bedingung ist nie erfüllt.
(E) Zuweisungen an den Elementtyp (hier auch int)
|
kleinstes=feld[aktuell] |
|
n-1 Wertzuweisungen |
|
kleinstes=feld[j] |
worst case:
best case:
|
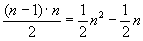
0 |
|
Zuweisungen in der unteren if-Abfrage |
worst case:
best case: |
2(n – 1)
0 |
(VI) Vergleiche von int-Elementen
- Überprüfung, ob aktuell den Endwert erreicht hat: n Vergleiche
- Überprüfung, ob j den Endwert erreicht hat: für jeden Wert von aktuell nimmt j eine Reihe von Werten an, die alle mit n verglichen werden. Man
erhält die Summanden
(n-1) + (n-2) + ¼ + 2
also
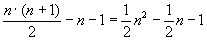
- Vergleiche, ob platz>aktuell: n-1
(VE) Vergleiche vom Element-Typ
In der Zeile feld[j]<kleinstes werden
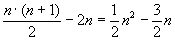 Vergleiche durchgeführt.
Vergleiche durchgeführt.
Zusammenfassung:
|
Art |
worst case |
best case |
|
(I) |
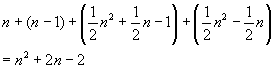 |
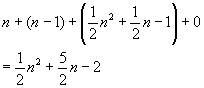 |
|
(E) |
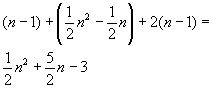 |
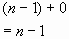
|
|
(VI) |
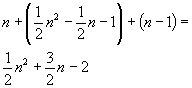 |
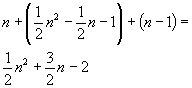 |
|
(VE) |
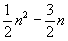 |
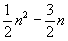 |
|
Summe: |
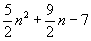 |
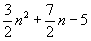 |
|
Landau: |
O (n2) |
O (n2) |
Also hat auch das gesamte Verfahren eine Ordnung
O(n2)!








© Ralph-Erich Hildebrandt, 04. Januar 2005
![]()